鸡尾酒排序

鸡尾酒排序

鸡尾酒排序（Cocktail Shaker Sort）是一种双向冒泡排序算法。它通过双向遍历数组，每次在两端交换元素，从而使得大值和小值可以同时移动到正确的位置。鸡尾酒排序比普通的冒泡排序在一些情况下更高效，尤其是对几乎已经排好序的数组。

鸡尾酒算法原理

  i. 先对数组从左到右进行升序的冒泡排序；
  ii. 再对数组进行从右到左的降序的冒泡排序；
  iii. 以此类推，持续的、依次的改变冒泡的方向，并不断缩小没有排序的数组范围；

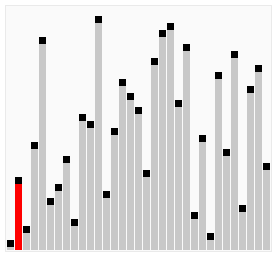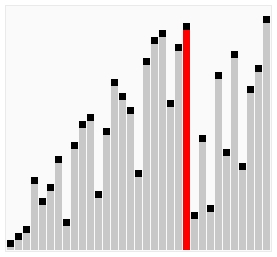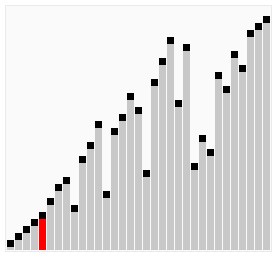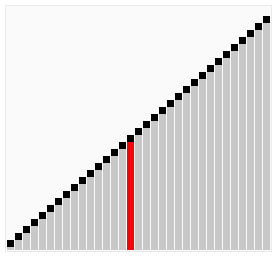
图示

鸡尾酒排序示例

以排序数组 [5, 3, 8, 4, 2] 为例，演示鸡尾酒排序的步骤。

第一步：从左到右遍历

比较并交换相邻元素，得到 [3, 5, 4, 2, 8]。

第二步：从右到左遍历

比较并交换相邻元素，得到 [3, 2, 4, 5, 8]。

第三步：重复上述步骤

继续从左到右遍历，得到 [2, 3, 4, 5, 8]。

此时数组已经有序，排序完成。

复杂度分析

鸡尾酒排序是冒泡排序的一种改进，并未有本质的改变，与冒泡排序的时间复杂度和空间复杂度相近，整体的性能都比较差。

• 顺序排列时，鸡尾酒排序时间复杂度为$O(n)$；
• 逆序排序时，鸡尾酒排序时间复杂度为$O(n^2)$；
• 当原始序列杂乱无序时，平均时间复杂度为$O(n^2)$。

鸡尾酒排序过程中，Swap函数需要一个临时变量temp进行两两交换，所需要的额外空间为1，因此空间复杂度为$O(1)$。

鸡尾酒排序是一种稳定的排序算法。

时间复杂度

• 最佳情况：$O(n)$。
• 最坏情况：$O(n^2)$。
• 平均情况：$O(n^2)$。

空间复杂度

• 空间复杂度：$O(1)$。

Java代码实现

import java.util.Arrays;

public class CocktailShakerSort {

    public static void cocktailShakerSort(int[] arr) {
        boolean swapped = true;
        int start = 0;
        int end = arr.length - 1;

        while (swapped) {
            swapped = false;

            // 从左到右遍历
            for (int i = start; i < end; i++) {
                if (arr[i] > arr[i + 1]) {
                    int temp = arr[i];
                    arr[i] = arr[i + 1];
                    arr[i + 1] = temp;
                    swapped = true;
                }
            }

            // 如果没有发生交换，数组已经有序
            if (!swapped) {
                break;
            }

            // 减少尾部索引
            end--;

            swapped = false;

            // 从右到左遍历
            for (int i = end - 1; i >= start; i--) {
                if (arr[i] > arr[i + 1]) {
                    int temp = arr[i];
                    arr[i] = arr[i + 1];
                    arr[i + 1] = temp;
                    swapped = true;
                }
            }

            // 增加起始索引
            start++;
        }
    }

    public static void main(String[] args) {
        int[] arr = {5, 3, 8, 4, 2};
        System.out.println("Given Array:");
        System.out.println(Arrays.toString(arr));

        // 调用鸡尾酒排序函数
        cocktailShakerSort(arr);

        System.out.println("Sorted Array:");
        System.out.println(Arrays.toString(arr));
    }
}