选择排序

选择排序

选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

工作原理

 

1. 首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，
2. 然后，再从剩余未排序元素中继续寻找最小（大）元素， 然后放到已排序序列的末尾。
3. 以此类推，直到所有元素均排序完毕。

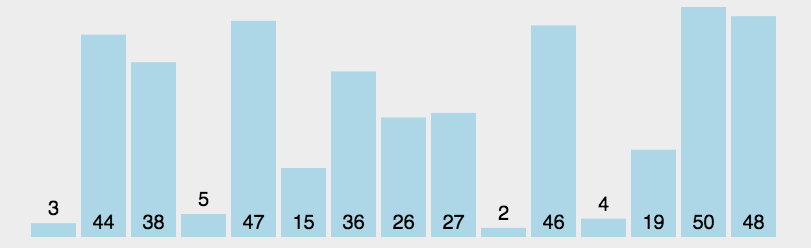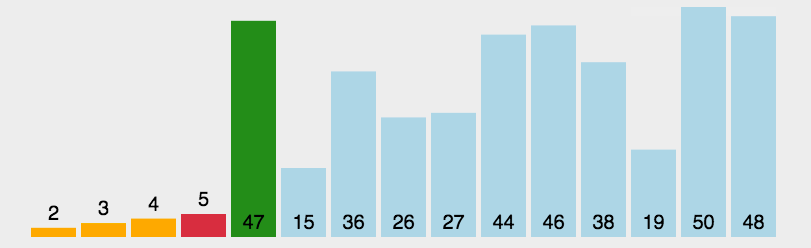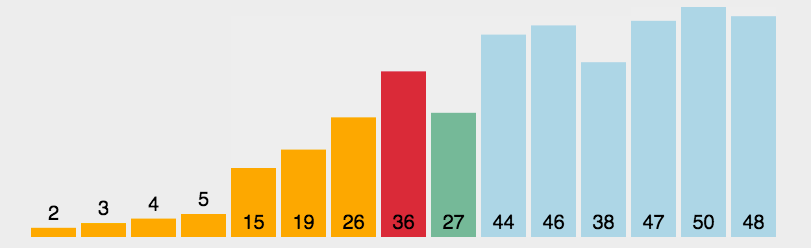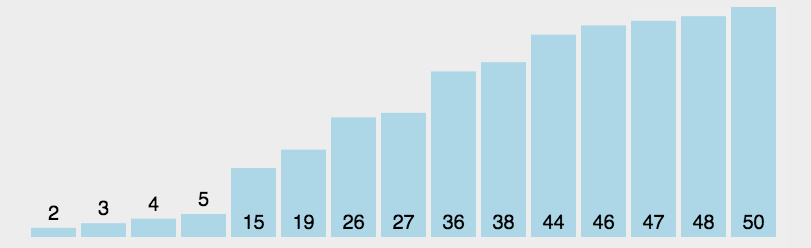
图示

示例

假设有一个待排序的列表：[64, 25, 12, 22, 11]

第一步

• 初始列表：[64, 25, 12, 22, 11]
• 找到最小元素 11，与第一个元素交换位置。 [11, 25, 12, 22, 64]

第二步

• 剩余未排序部分：[25, 12, 22, 64]
• 找到最小元素 12，与第二个元素交换位置。 [11, 12, 25, 22, 64]

第三步

• 剩余未排序部分：[25, 22, 64]
• 找到最小元素 22，与第三个元素交换位置。 [11, 12, 22, 25, 64]

第四步

• 剩余未排序部分：[25, 64]
• 找到最小元素 25，与第四个元素交换位置。 [11, 12, 22, 25, 64]

第五步

• 剩余未排序部分：[64]
• 已排序完成。

复杂度分析

交换次数$𝑂(𝑛)$，最好情况是，已经有序，交换0次；最坏情况是，逆序，交换$𝑛-1$次。 交换次数比冒泡排序较少，由于交换所需CPU时间比比较所需的CPU时间多，$𝑛$值较小时，选择排序比冒泡排序快。

原地操作几乎是选择排序的唯一优点，当空间复杂度要求较高时，可以考虑选择排序；实际适用的场合非常罕见。

• 时间复杂度为 $O(n^2)$、非自适应排序：外循环共 $n-1$ 轮，第一轮的未排序区间长度为 $n$ ，最后一轮的未排序区间长度为 $2$ ，即各轮外循环分别包含 $n$、$n-1$、$\dots$、$3$、$2$ 轮内循环，求和为 $\frac{(n-1)(n+2)}{2}$ 。

• 空间复杂度为 $O(1)$、原地排序：指针 $i$ 和 $j$ 使用常数大小的额外空间。

• 非稳定排序相等的元素的右边，导致两者的相对顺序发生改变。

时间复杂度

• 最坏情况时间复杂度：$O(n^2)$
• 平均情况时间复杂度：$O(n^2)$
• 最好情况时间复杂度：$O(n^2)$

空间复杂度

• 空间复杂度：$O(1)$

代码实现

以下是选择排序的Java实现代码：

public class SelectionSort {
    public static void selectionSort(int[] arr) {
        int n = arr.length;

        // 一一选择未排序部分中的最小元素
        for (int i = 0; i < n-1; i++) {
            // 假设当前 i 位置上的元素为最小值
            int minIdx = i;

            // 在未排序部分中找到最小元素
            for (int j = i+1; j < n; j++) {
                if (arr[j] < arr[minIdx]) {
                    minIdx = j;
                }
            }

            // 将找到的最小元素与当前 i 位置上的元素交换
            int temp = arr[minIdx];
            arr[minIdx] = arr[i];
            arr[i] = temp;
        }
    }

    public static void main(String[] args) {
        int[] arr = {64, 25, 12, 22, 11};
        selectionSort(arr); 
        for (int i : arr) {
            System.out.print(i + " "); // 输出排序后的数组
        }
    }
}