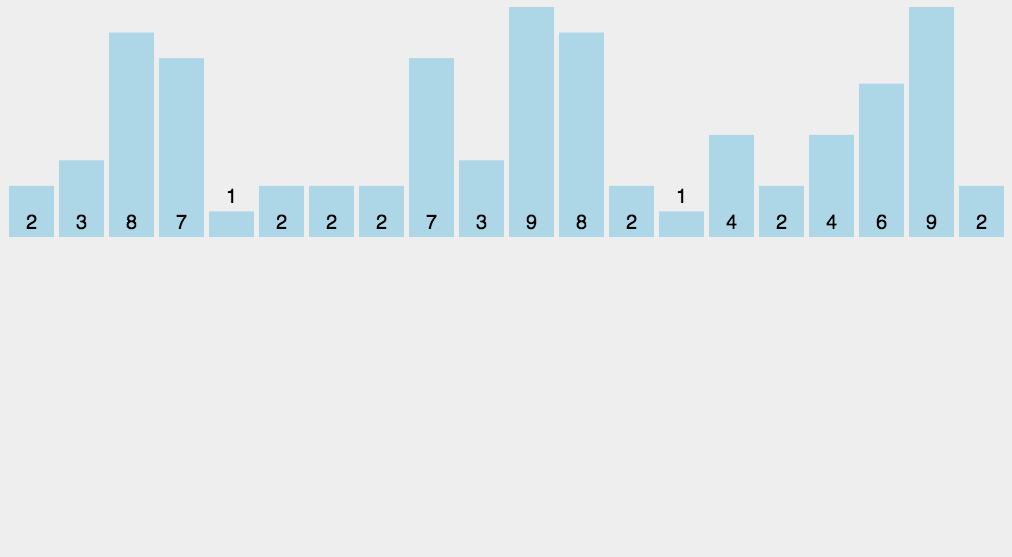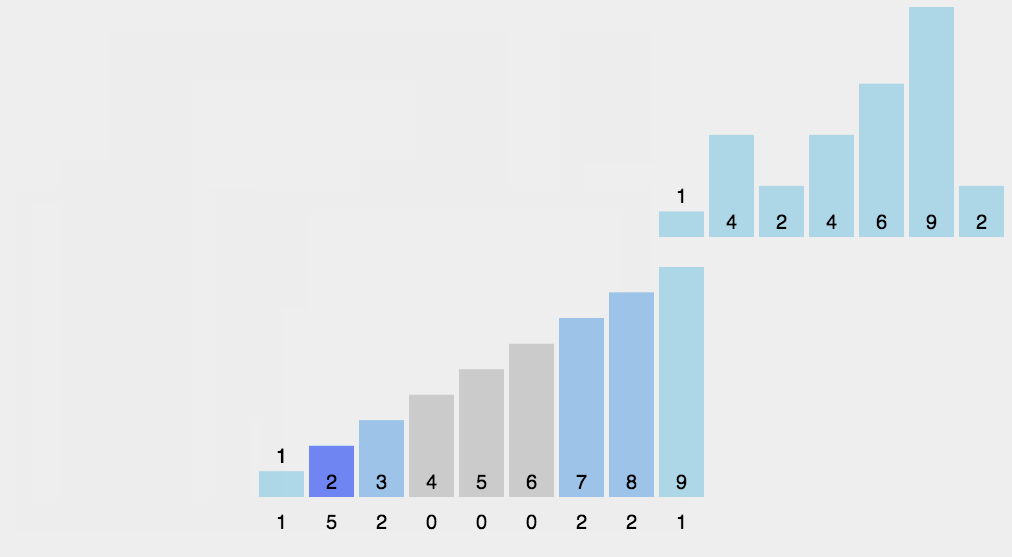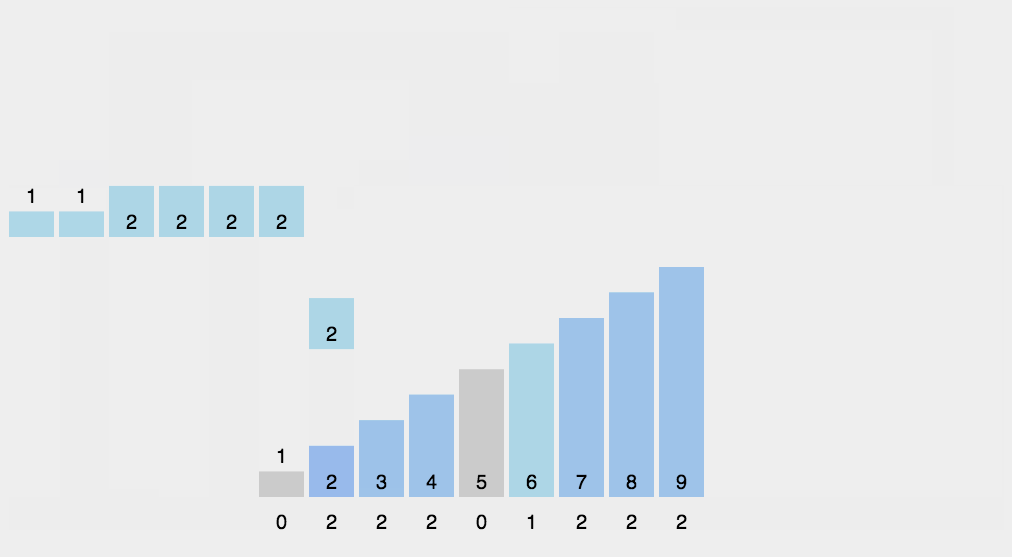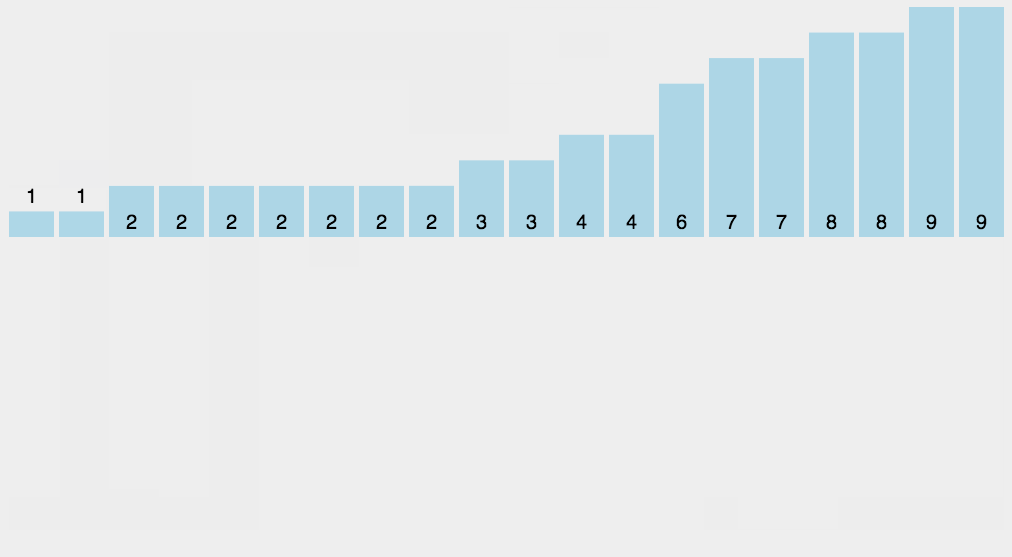计数排序

计数排序

计数排序（Counting Sort）是一种线性时间复杂度的排序算法。它适用于排序一定范围内的整数，特别是当范围不大时，表现非常高效。

计数排序的原理

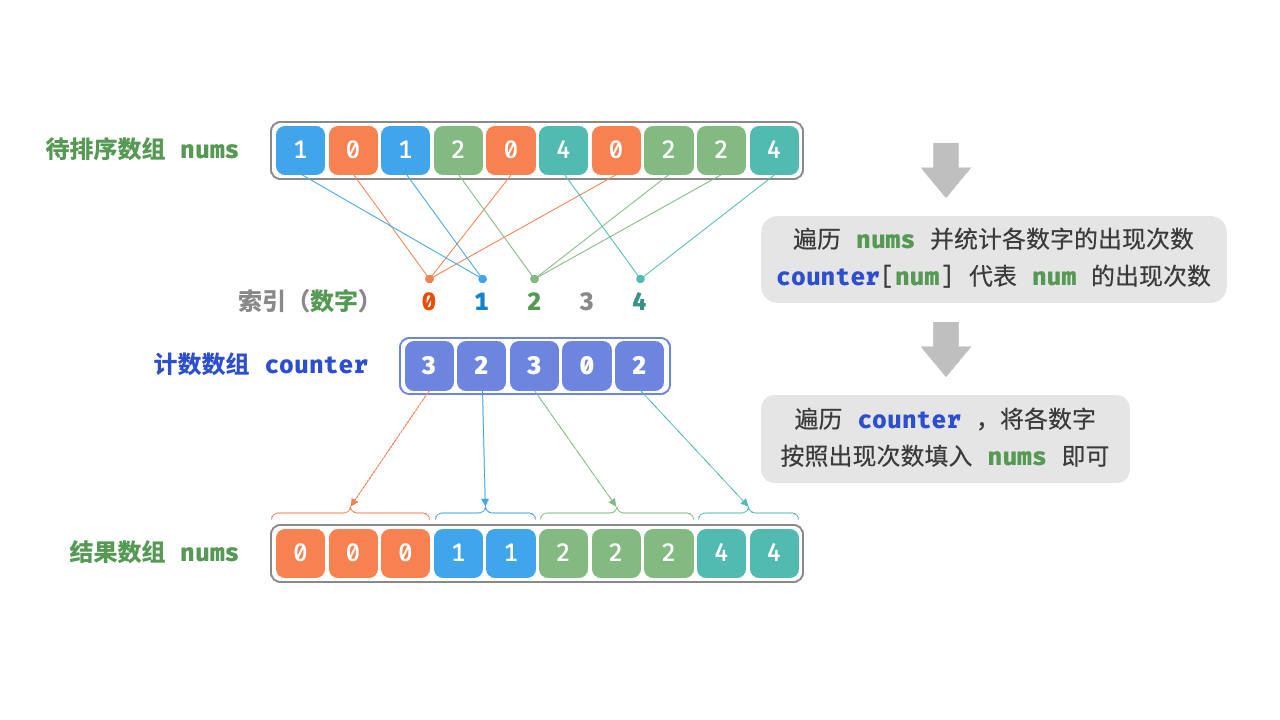
计数排序的主要思想是通过统计每个元素的出现次数，计算出每个元素在排序后数组中的位置，从而实现排序。计数排序适用于数据范围相对较小且数据分布比较均匀的情况。

图示

计数排序的步骤

1. 找出数组中的最大值和最小值：确定数据的范围。
2. 创建计数数组：计数数组的大小为最大值和最小值之间的差加1，用于记录每个元素的出现次数。
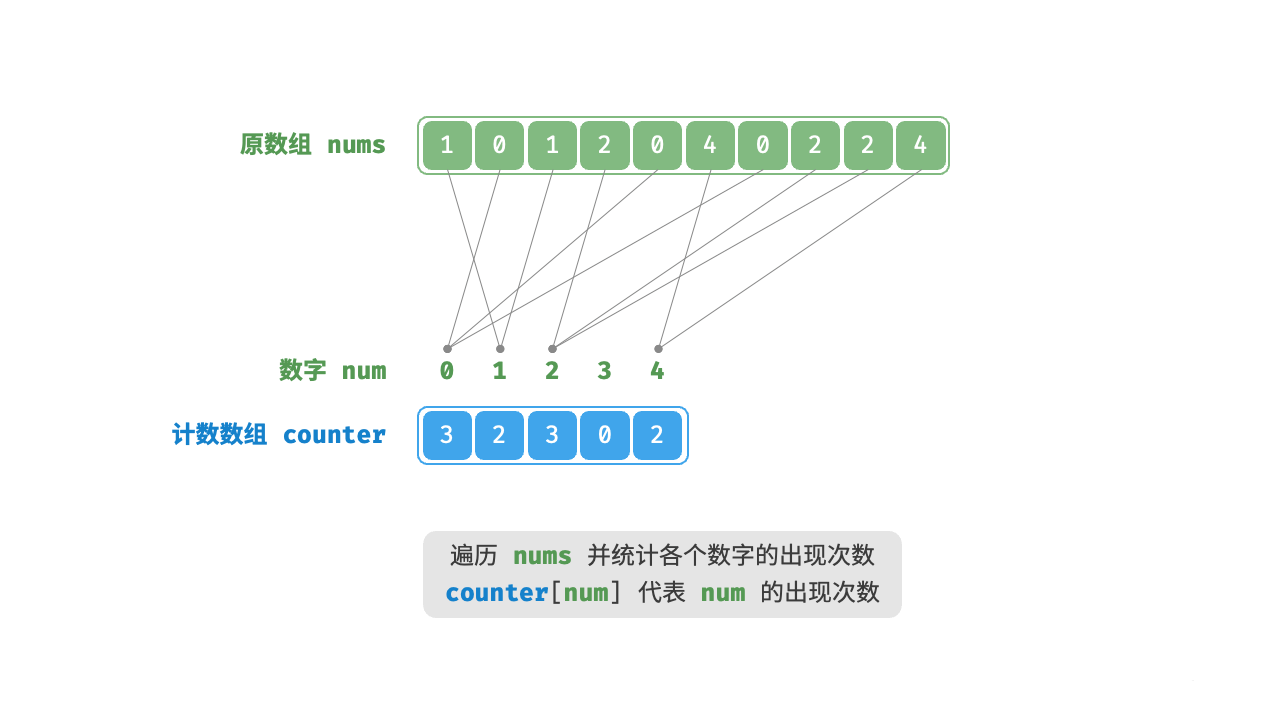
3. 统计每个元素的出现次数：遍历待排序数组，填充计数数组。
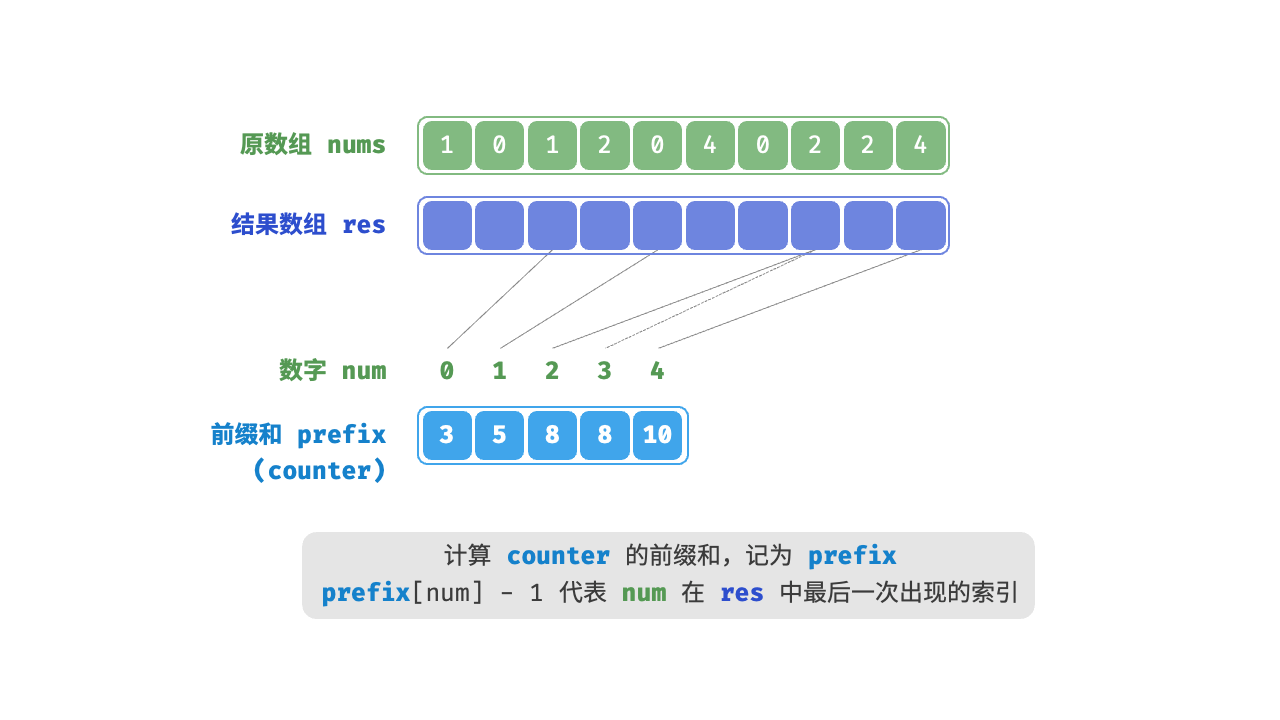
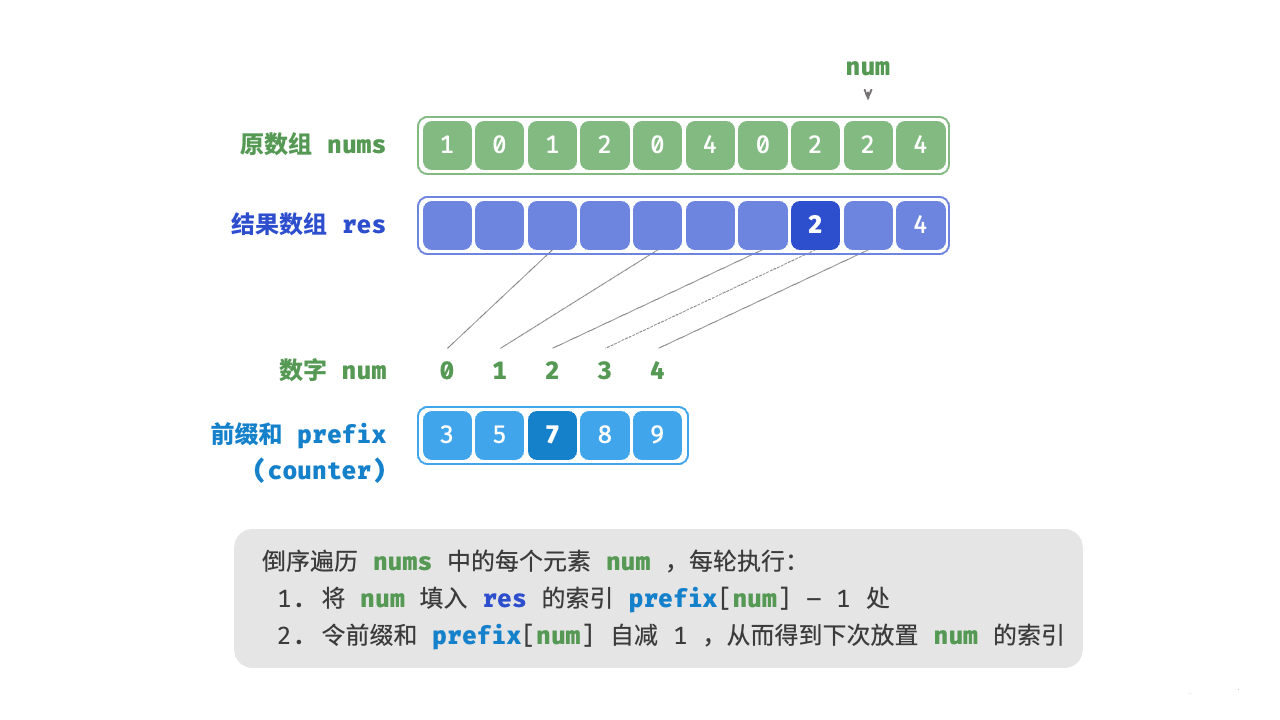
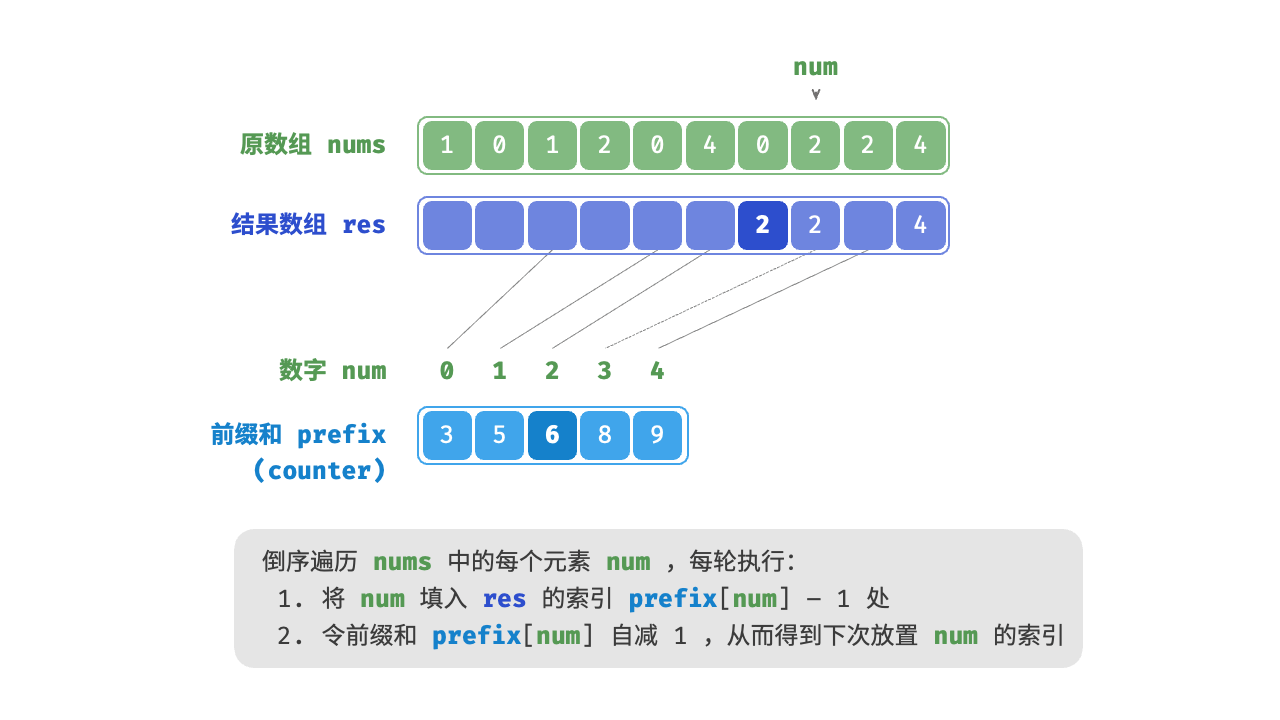
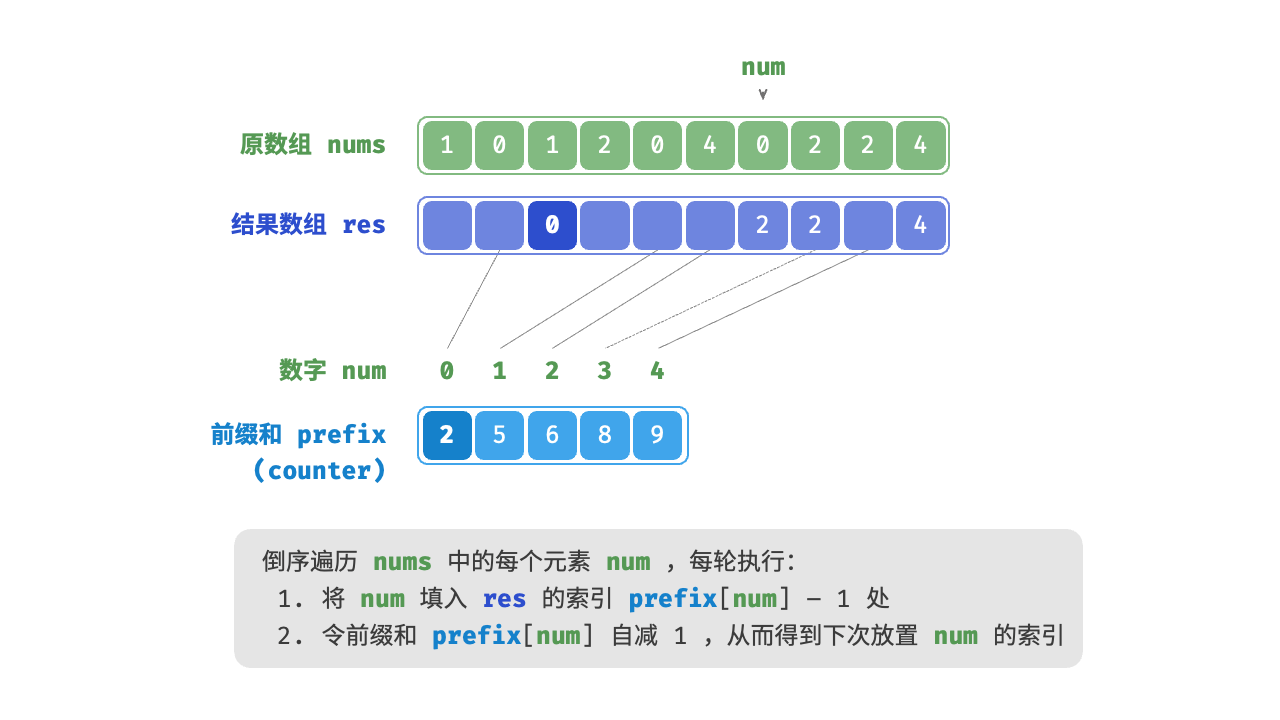
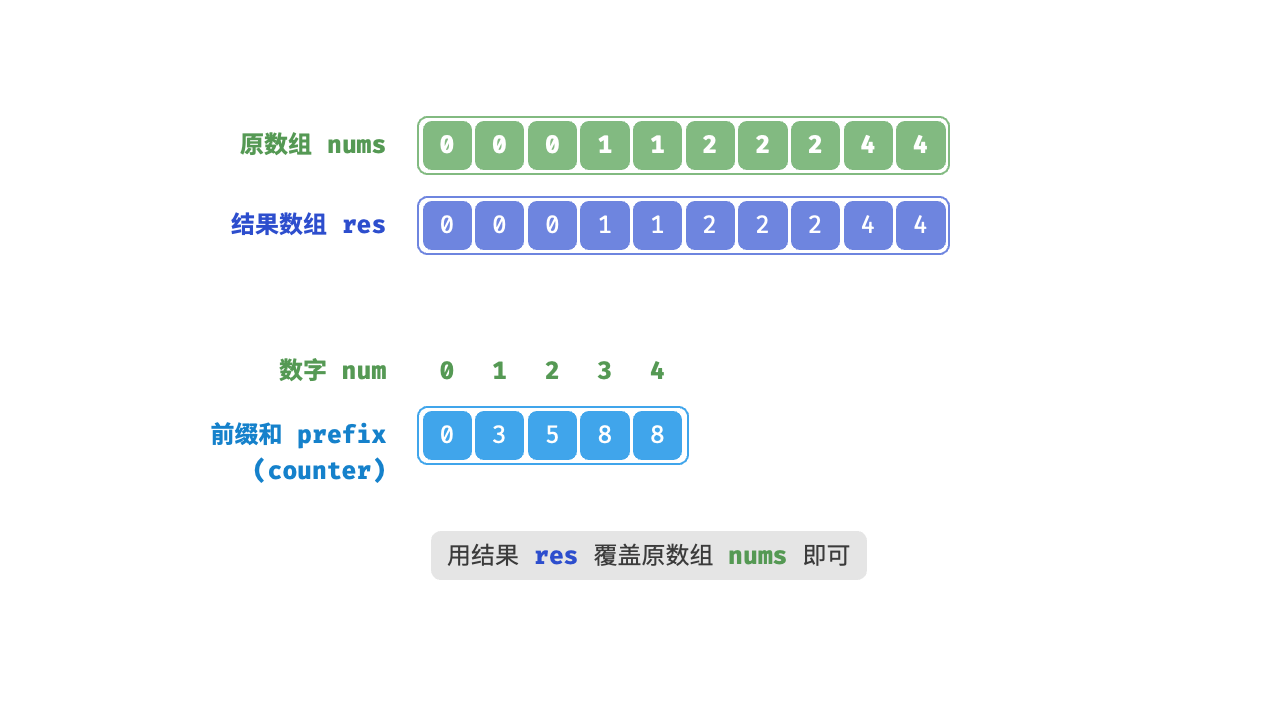
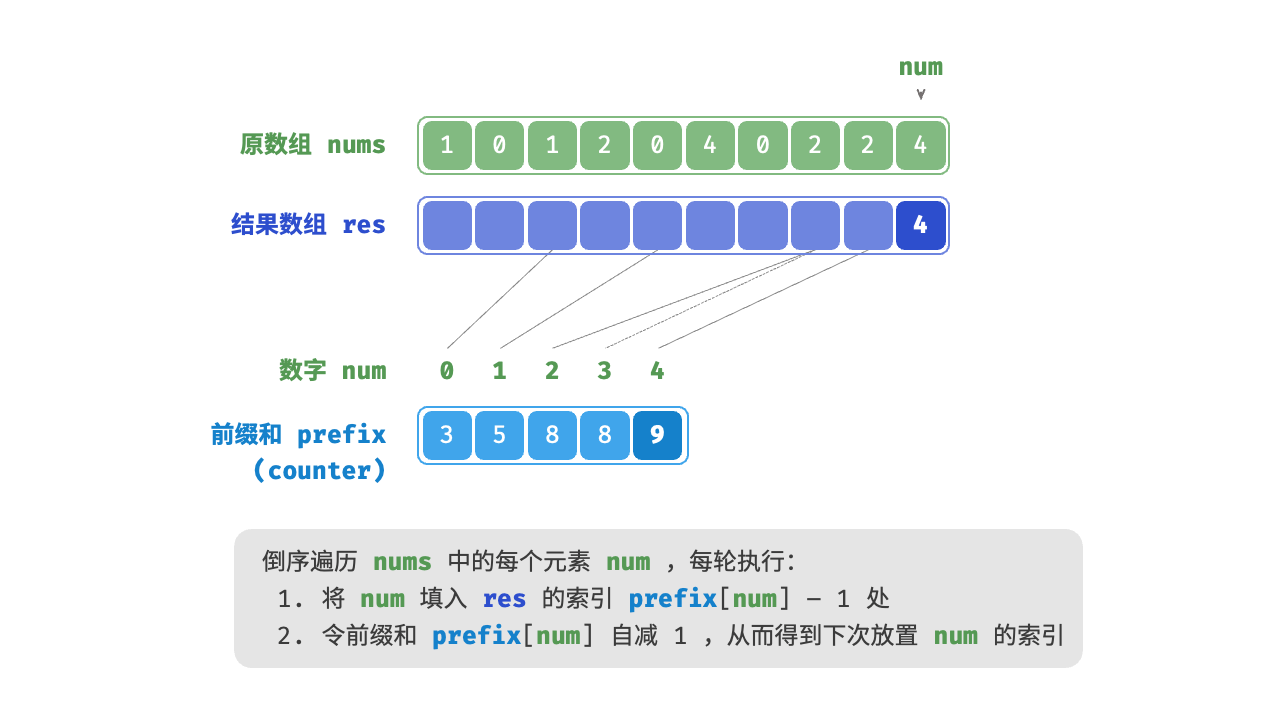
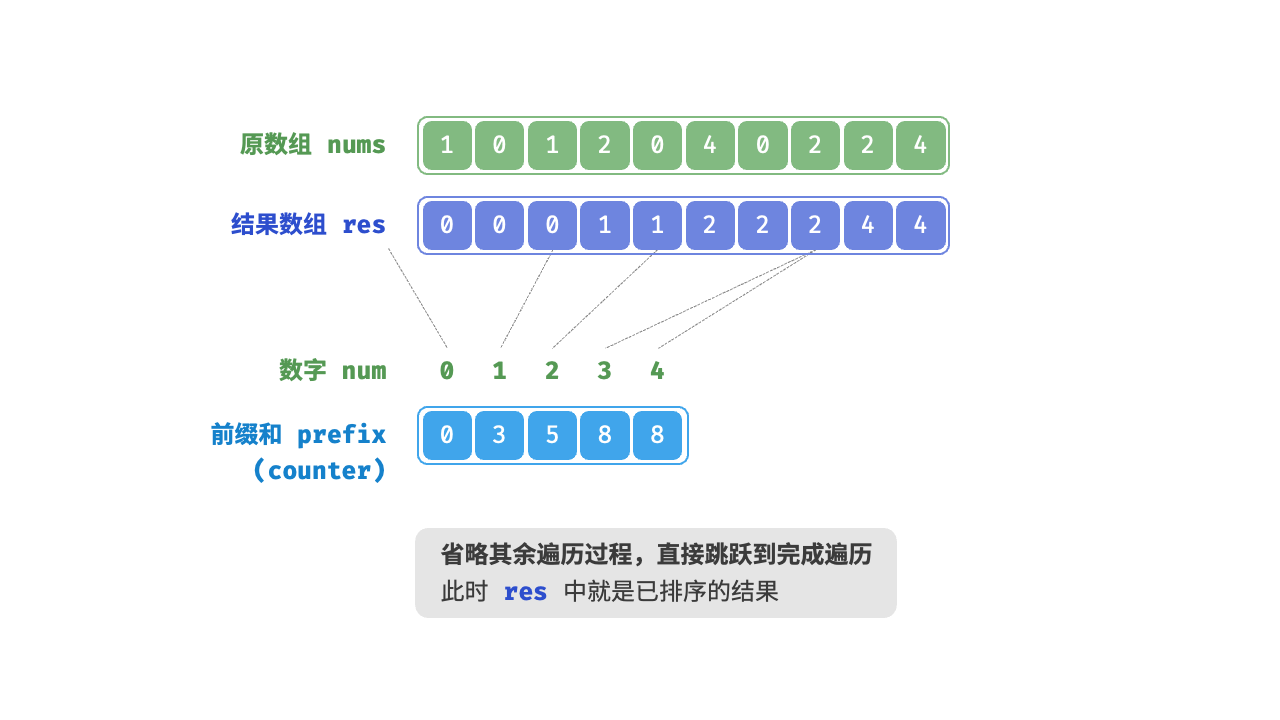
4. 计算元素的最终位置：对计数数组进行累加处理，得到每个元素在排序后数组中的位置。前缀和具有明确的意义，prefix[num] - 1 代表元素 num 在结果数组 res 中最后一次出现的索引。这个信息非常关键，因为它告诉我们各个元素应该出现在结果数组的哪个位置。
5. 构建输出数组：根据计数数组的信息，将原数组的元素放到正确的位置上。
6. 复制到原数组：将输出数组复制回原数组，完成排序。

计数排序示例

step1

step2

step3

step4

step5

step6

step7

step8

复杂度分析

当输入的元素是𝑛个0到𝑘之间的整数时，它的运行时间是 $\Theta (n+k)$。计数排序不是比较排序，因此不被 $\Omega (n\log n)$的下界限制。

• 时间复杂度为 $O(n + k)$、非自适应排序 ：涉及遍历 nums 和遍历 counte ，都使用线性时间。一般情况下 $n \gg k$ ，时间复杂度趋于 $O(n)$ 。
• 空间复杂度为 $O(n + k)$、非原地排序：借助了长度分别为 $n$ 和 $m$ 的数组 res 和 counte 。
• 稳定排序：由于向 res 中填充元素的顺序是“从右向左”的，因此倒序遍历 nums 可以避免改变相等元素之间的相对位置，从而实现稳定排序。实际上，正序遍历 nums 也可以得到正确的排序结果，但结果是非稳定的。

时间复杂度

• 最佳情况：$O(n+k)$。
• 最坏情况：$O(n+k)$。
• 平均情况：$O(n+k)$。

空间复杂度

• 空间复杂度：$O(n+k)$。

局限性

计数排序非常巧妙，仅通过统计数量就可以实现高效的排序。然而，使用计数排序的前置条件相对较为严格。

计数排序只适用于非负整数。若想将其用于其他类型的数据，需要确保这些数据可以转换为非负整数，并且在转换过程中不能改变各个元素之间的相对大小关系。例如，对于包含负数的整数数组，可以先给所有数字加上一个常数，将全部数字转化为正数，排序完成后再转换回去。

计数排序适用于数据量大但数据范围较小的情况。比如，在上述示例中 $k$ 不能太大，否则会占用过多空间。而当 $n \ll k$ 时，计数排序使用 $O(k)$ 时间，可能比 $O(n \log n)$ 的排序算法还要慢。

Java代码实现

import java.util.Arrays;

public class CountingSort {

    public static void countingSort(int[] nums) {
        int n = nums.length;

        // 找出数组中的最大值和最小值
        int max = Arrays.stream(nums).max().getAsInt();
        int min = Arrays.stream(nums).min().getAsInt();

        // 创建计数数组，大小为 (max - min + 1)
        int range = max - min + 1;
        // counter[num] 代表 num 的出现次数
        int[] counter = new int[range];
        // 初始化数组 res 用于记录结果
        int[] res = new int[n];

        // 统计每个元素的出现次数
        for (int num : nums) {
            counter[num - min]++;
        }

        // 计算元素的最终位置（累加处理）
        // 求 counter 的前缀和，将“出现次数”转换为“尾索引”
        // 即 counter[num]-1 是 num 在 res 中最后一次出现的索引
        for (int i = 1; i < counter.length; i++) {
            counter[i] += counter[i - 1];
        }
		
        // 倒序遍历 arr ，将各元素填入结果数组 res 
        for (int i = n - 1; i >= 0; i--) {
	        int num = nums[i] - min; 
	        // 将 num 放置到对应索引处 
	        res[counter[num] - 1] = num;
	        // 令前缀和自减 1 ，得到下次放置 num 的索引 
	        counter[num]--; 
        }

        // 将输出数组复制回原数组
        System.arraycopy(res, 0, nums, 0, n);
    }

    public static void main(String[] args) {
        int[] arr = {4, 2, 2, 8, 3, 3, 1};
        System.out.println("Given Array:");
        System.out.println(Arrays.toString(arr));

        // 调用计数排序函数
        countingSort(arr);

        System.out.println("Sorted Array:");
        System.out.println(Arrays.toString(arr));
    }
}