斐波那契数

在数学上，斐波那契数是以递归的方法来定义：

• $F_{0}=0$
• $F_{1}=1$
• $F_{n}=F_{n-1}+F_{n-2}$ $(n\geqq 2)$

用白话文来说，就是斐波那契数列由0和1开始，之后的斐波那契数就是由之前的两数相加而得出。首几个斐波那契数是：

1、1、2、3、5、8、13、21、34、55、89、144、233、377、610、987 …..

特别指出：0 不是第一项，而是第零项 $F_{0}$。

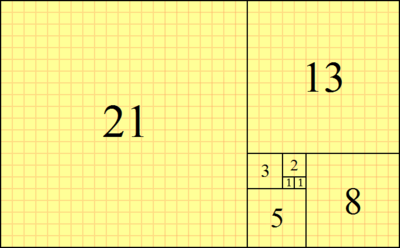
图示

公约数和整除关系

• $F_{n}$整除$F_{m}$，当且仅当$n$整除$m$，其中$n\geqq 3$。
• $\gcd(F_{m},F_{n})=F_{\gcd(m,n)}$
• 任意连续三个菲波那契数两两互素，亦即，对于每一个$n$，$\mathrm{gcd}(F_{n},F_{n+1})=\mathrm{gcd}(F_{n},F_{n+2})=\mathrm{gcd}(F_{n+1},F_{n+2})=1$

• 斐波那契素数

在斐波那契数列中，有素数：2, 3, 5, 13, 89, 233, 1597, 28657, 514229, 433494437, 2971215073, 99194853094755497, 1066340417491710595814572169, 19134702400093278081449423917……

截至2015年，已知最大的斐波那契素数是第104911个斐波那契数，一共有21925个十进制位。不过，人们仍不知道是不是有无限个斐波那契素数。

如公约数和整除关系所述，$F_{kn}$总能被$F_{n}$整除，故除$F_{4}=3$之外，任何斐氏素数的下标必同为素数。由于存在任意长的一列连续合数，斐氏数列中亦能找到连续任意多项全为合数。

大于$F_{6}=8$的斐氏数，必不等于素数加一或减一。

模n的周期性

斐波那契数列各项模 $n$的余数构成周期数列，其最小正周期称为皮萨诺周期，至多为$6n$。皮萨诺周期对不同$n$值的通项公式仍是未解问题，其中一步需要求出某个整数（同余意义下）或二次有限域元素的乘法阶数。不过，对固定的$n$，求解模$n$的皮萨诺周期是周期检测问题的特例。