快速排序
快速排序(Quick Sort)是一种高效的排序算法,采用分治法策略,通过选择一个基准(pivot),将数组划分为两部分,然后递归地对两部分分别进行排序。
快速排序
快速排序(Quick Sort)是一种高效的排序算法,采用分治法策略,通过选择一个基准(pivot),将数组划分为两部分,然后递归地对两部分分别进行排序。快速排序有很多不同的版本,它们以不同的方式选择枢轴。
- 总是选择第一个元素作为 pivot。
- 总是选择最后一个元素作为 pivot。
- 随机选一个元素作为 pivot。
- 选择中值作为 pivot。
QuickSort 中的关键步骤是 partition()。在数组中选择的一个元素为支点(pivot), 把所有小于 pivot 的元素放到 pivot 左面, 大于 pivot 的放右边。这样数组 x[n] 会被划分成3个部分:
x[0] , ... , x[pivot - 1]x[pivot]x[pivot+1] , ... , x[n]
快速排序的原理
- 选择基准:从数组中选择一个元素作为基准。
- 分区:将数组分为两个部分,使得左边部分的所有元素都小于等于基准元素,右边部分的所有元素都大于等于基准元素。
- 递归排序:递归地对基准元素左边和右边的部分进行排序。
快速排序的步骤
- 选择基准元素:选择数组的最后一个元素作为基准元素。
- 分区过程:
- 初始化基准元素的正确位置索引
i为left - 1。 - 遍历子数组,将小于或等于基准元素的元素移动到基准元素的左边。
- 将基准元素放到正确的位置。
- 初始化基准元素的正确位置索引
- 递归排序:递归地对左边和右边的子数组进行排序。
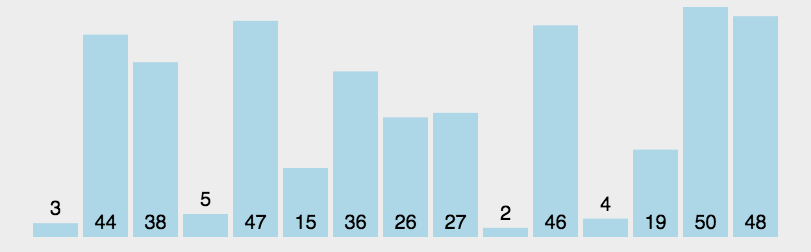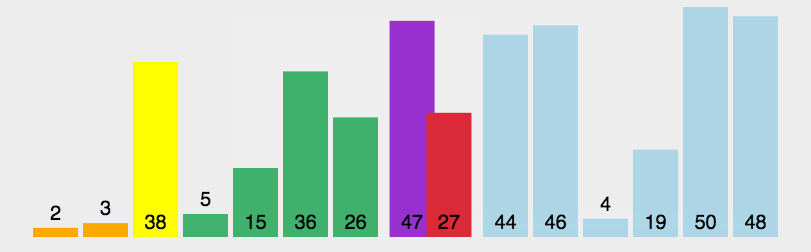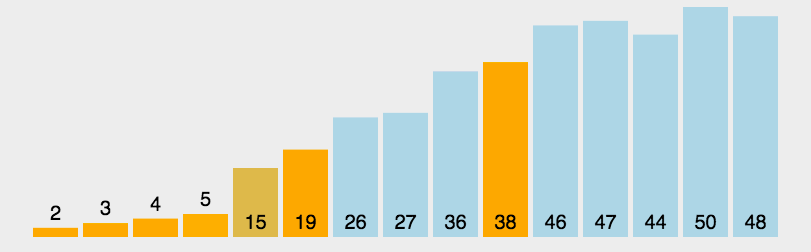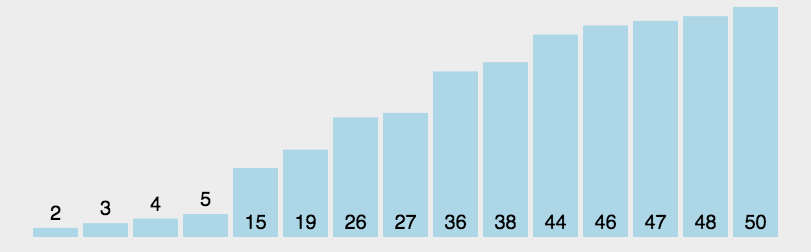
图示
示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
//right = arr.lenght-1
public static int partition(int[] arr, int left, int right) {
// 选择最右边的元素作为基准
int pivot = arr[right];
// 较小元素的索引并表示
// 到目前为止找到的枢轴的正确位置
int i = left - 1;
for (int j = left; j < right; j++) {
// 如果当前元素小于或等于基准
if (arr[j] <= pivot) {
// 基准元素的正确位置向右移动
i++;
// 交换当前元素和基准元素
swap(arr, i, j);
}
}
// 将基准元素放到正确的位置
swap(arr, i + 1, right);
// 返回基准元素的位置
return i + 1;
}
arr[] = {10, 80, 30, 90, 40, 50, 70}
Indexes: 0 1 2 3 4 5 6
low = 0, high = 6, pivot = arr[h] = 70
初始化较小元素的索引,i = -1
从 j = low 到 high-1 遍历元素
j = 0 :由于 arr[j] <= pivot,执行 i++ 并交换(arr[i], arr[j])
i = 0
arr[] = {10, 80, 30, 90, 40, 50, 70} //交换0,0 。 没有变化 相同
j = 1 :由于 arr[j] > pivot,不执行任何操作
i = 0
arr[] = {10, 80, 30, 90, 40, 50, 70} // i 和 arr[] 没有变化
j = 2 :由于 arr[j] <= pivot,执行 i++ 并交换(arr[i], arr[j])
i = 1
arr[] = {10, 30, 80, 90, 40, 50, 70} // 交换2,1 。交换 80 和 30
j = 3 :由于 arr[j] > pivot,不执行任何操作
i = 1
arr[] = {10, 30, 80, 90, 40, 50, 70}// i 和 arr[] 没有变化
j = 4 :由于 arr[j] <= pivot,执行 i++ 并交换(arr[i], arr[j])
i = 2
arr[] = {10, 30, 40, 90, 80, 50, 70} // 交换4,2。交换 80 和 40
j = 5 :由于 arr[j] <= pivot,执行 i++ 并将 arr[i] 与 arr[j] 交换
i = 3
arr[] = {10, 30, 40, 50, 80, 90, 70} //交换5,3 。交换 90 和 50
此时j++=6 不符合<6的要求,退出循环.
最后我们通过交换将pivot放置在正确的位置
arr[i+1] 和 arr[right] (或pivot)
arr[] = {10, 30, 40, 50, 70, 90, 80} //交换4,7。交换 80 和 70
现在 70 处于正确的位置.所有元素小于 70 在其之前,所有大于 70 的元素在其之后.
复杂度分析
时间复杂度为 $O(n \log n)$、自适应排序 在最坏的情况下,第 1 趟排序经过 $𝑛−1$ 次比较以后,第 1个元素仍然确定在原来的位置上,并得到 1 个长度为 $n−1$ 的子数组。第 2 趟排序进过 $𝑛−2$ 次比较以后,将第 2 个元素确定在它原来的位置上,又得到 1 个长度为 $𝑛−2$ 的子数组。 最终总的比较次数为$(n−1)+(n−2)+…+1=\frac {n(n-1)}{2}$。 因此这种情况下的时间复杂度为 $𝑂(𝑛^2)$。
在最好的情况。如果每次我们选中的基准数恰好能将当前数组平分为两份,也就是刚好取到当前数组的中位数。每一次都将数组从 𝑛 个元素变为 $\frac{n}{2}$ 个元素。此时的时间复杂度公式为$T(n)=2T(\frac {n}{2})+\Theta (n)$。 解决这种关系式类型的标准数学归纳法技巧告诉我们结果为$T(n)=O(n\log n)$ 事实上,并不需要把数列如此精确地分割;即使如果每个基准值将元素分开为99%在一边和1%在另一边,调用的深度仍然限制在$100\log n$,所以全部执行时间依然是 $O(n\log n)$。
而在平均情况下,我们可以从当前数组中随机选择一个元素作为基准数。这样,每一次选择的基准数可以看做是等概率随机的。其期望时间复杂度为 $𝑂(𝑛\log𝑛)$,也就是平均时间复杂度。
空间复杂度为 $O(n)$、原地排序 空间复杂度主要是由于递归调用造成的栈空间使用。 在最坏情况下,递归的层数为n,此时空间复杂度为$O(n)$。 在平均情况下,递归的层数为$\log n$,此时空间复杂度为$O(\log n)$。
非稳定排序:在哨兵划分的最后一步,基准数可能会被交换至相等元素的右侧。
时间复杂度
- 最佳情况:$O(n\log n)$。
- 最坏情况:$O(n^2)$。
- 平均情况:$O(n\log n)$。
空间复杂度
- 最好情况:$O(\log n)$。
- 最坏情况:$O(n)$
- 平均情况:$O(\log n)$。
快速排序的代码实现(Java)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
public class QuickSort {
// 主排序函数
public static void quickSort(int[] arr, int left, int right) {
if (left < right) {
// 找到基准元素的位置
int pivotIndex = partition(arr, left, right);
// 递归地排序基准元素左边的部分
quickSort(arr, left, pivotIndex - 1);
// 递归地排序基准元素右边的部分
quickSort(arr, pivotIndex + 1, right);
}
}
// 分区函数
public static int partition(int[] arr, int left, int right) {
// 选择最右边的元素作为基准
int pivot = arr[right];
// 较小元素的索引并表示
// 到目前为止找到的枢轴的正确位置
int i = left - 1;
for (int j = left; j < right; j++) {
// 如果当前元素小于或等于基准
if (arr[j] <= pivot) {
// 基准元素的正确位置向右移动
i++;
// 交换当前元素和基准元素
swap(arr, i, j);
}
}
// 将基准元素放到正确的位置
swap(arr, i + 1, right);
// 返回基准元素的位置
return i + 1;
}
// 交换函数
public static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
// 主函数
public static void main(String[] args) {
int[] arr = {38, 27, 43, 3, 9, 82, 10};
System.out.println("Given Array:");
for (int num : arr) {
System.out.print(num + " ");
}
System.out.println();
// 调用快速排序函数
quickSort(arr, 0, arr.length - 1);
System.out.println("\nSorted Array:");
for (int num : arr) {
System.out.print(num + " ");
}
System.out.println();
}
}