归并排序
归并排序(Merge Sort)是一种基于分治法的有效排序算法。它将一个列表分成较小的子列表,对每个子列表进行排序,然后合并这些子列表以产生一个有序列表。
归并排序
归并排序原理
归并排序(Merge Sort)是一种基于分治法(Divide and Conquer)的有效排序算法。它将一个列表分成较小的子列表,对每个子列表进行排序,然后合并这些子列表以产生一个有序列表。
1
2
3
采用分治法:
分割:递归地把当前序列平均分割成两半。
集成:在保持元素顺序的同时将上一步得到的子序列集成到一起(归并)。
工作原理
- 分割:将列表分成两个子列表。
- 递归排序:对每个子列表递归地进行归并排序。
- 合并:将两个有序的子列表合并成一个有序列表。
归并操作
归并操作(merge),也叫归并算法,指的是将两个已经排序的序列合并成一个序列的操作。归并排序算法依赖归并操作。
递归法(Top-down)
- 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
- 设定两个指针,最初位置分别为两个已经排序序列的起始位置
- 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
- 重复步骤3直到某一指针到达序列尾
- 将另一序列剩下的所有元素直接复制到合并序列尾
迭代法(Bottom-up)
原理如下(假设序列共有$𝑛$个元素):
- 将序列每相邻两个数字进行归并操作,形成$𝑐𝑒𝑖𝑙(𝑛/2)$个序列,排序后每个序列包含两/一个元素
- 若此时序列数不是1个则将上述序列再次归并,形成$𝑐𝑒𝑖𝑙(𝑛/4)$个序列,每个序列包含四/三个元素
- 重复步骤2,直到所有元素排序完毕,即序列数为1
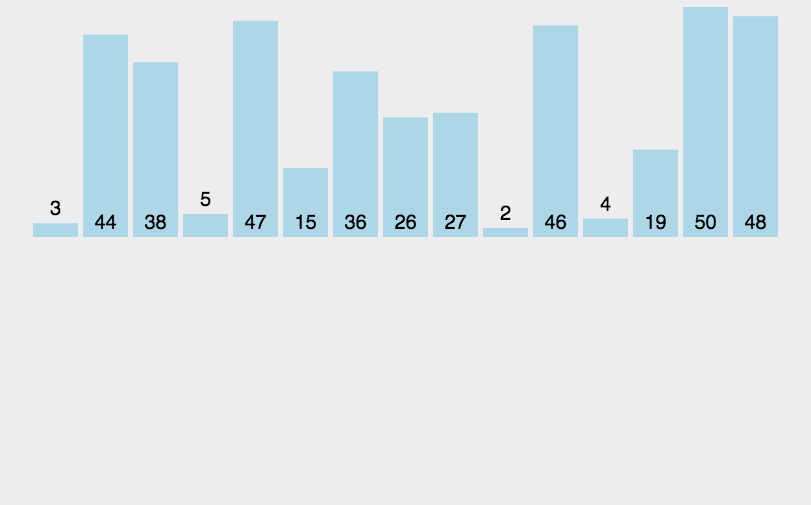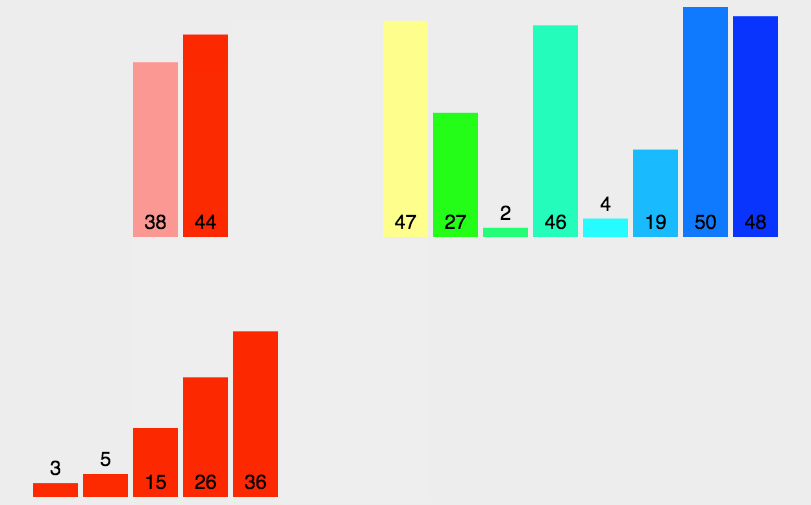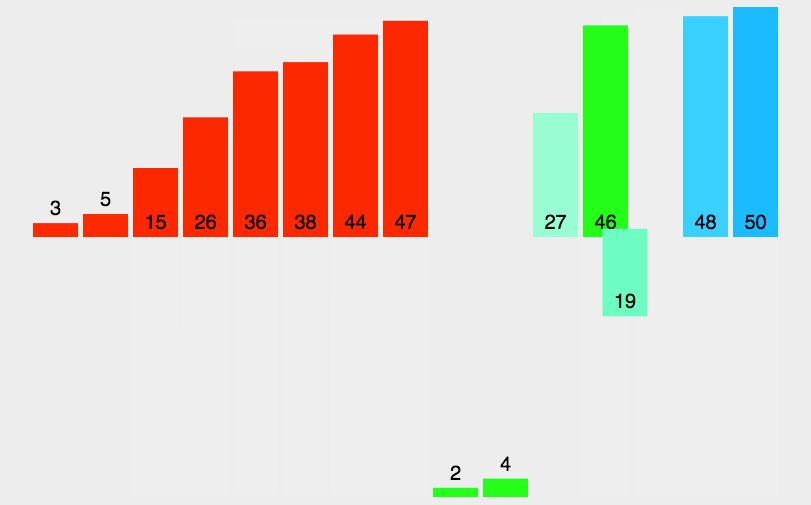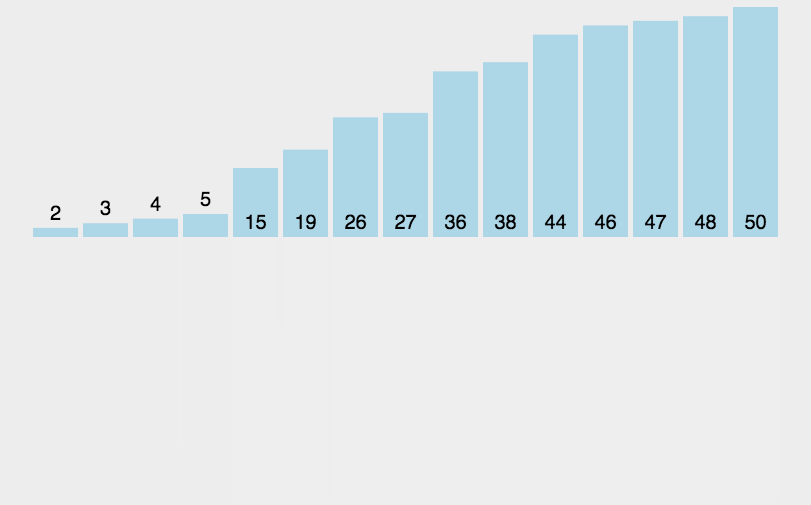
图示
示例
假设有一个待排序的列表:[38, 27, 43, 3, 9, 82, 10]
第一步:分割
- 将列表分割成两个子列表:[38, 27, 43] 和 [3, 9, 82, 10]
第二步:递归排序
- 继续将子列表分割,直到每个子列表只有一个元素。
- [38], [27], [43], [3], [9], [82], [10]
第三步:合并
- 将单个元素的子列表合并成有序子列表。
- [27, 38], [3, 43], [9, 82], [10]
- 继续合并,直到得到最终的有序列表。
- [3, 27, 38, 43], [9, 10, 82]
- [3, 9, 10, 27, 38, 43, 82]
复杂度分析
时间复杂度为 $O(n \log n)$、非自适应排序:划分产生高度为 $\log n$ 的递归树,每层合并的总操作数量为 $n$ ,因此总体时间复杂度为 $O(n \log n)$ 。
空间复杂度为 $O(n)$、非原地排序:递归深度为 $\log n$ ,使用 $O(\log n)$ 大小的栈帧空间。合并操作需要借助辅助数组实现,使用 $O(n)$ 大小的额外空间。
- 稳定排序:在合并过程中,相等元素的次序保持不变。
时间复杂度
- 最坏情况时间复杂度:$O(n\log n)$
- 平均情况时间复杂度:$O(n\log n)$
- 最好情况时间复杂度:$O(n\log n)$
空间复杂度
- 空间复杂度:$O(n)$
代码实现
递归版与迭代版
递归版
实现方式:
- 递归版归并排序使用递归函数来实现分治算法。
- 它将数组分成两半,分别对每一半进行排序,然后合并排序好的两半。
优点:
- 代码简洁、易于理解和实现。
- 直接利用函数调用栈管理递归过程。
缺点:
- 递归调用会占用函数调用栈空间,对于大型数组可能会导致栈溢出。
迭代版
实现方式:
- 迭代版归并排序使用迭代方法来实现分治算法。
- 它从较小的子数组开始逐步合并,直到整个数组有序。
优点:
- 不会出现栈溢出的问题。
- 可以更好地控制内存使用。
缺点:
- 实现相对复杂,代码冗长。
递归版实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
public class MergeSort {
// 合并两个有序子数组 arr[l..m] 和 arr[m+1..r]
public static void merge(int[] arr, int l, int m, int r) {
// 找到两个子数组的大小
int n1 = m - l + 1;
int n2 = r - m;
// 创建临时数组
int[] L = new int[n1];
int[] R = new int[n2];
// 复制数据到临时数组 L 和 R
for (int i = 0; i < n1; ++i)
L[i] = arr[l + i];
for (int j = 0; j < n2; ++j)
R[j] = arr[m + 1 + j];
// 初始索引
int i = 0, j = 0, k = l;
// 合并临时数组 L 和 R 回到 arr[l..r]
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = R[j];
j++;
}
k++;
}
// 复制 L 中剩余的元素(如果有)
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
// 复制 R 中剩余的元素(如果有)
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
// 主函数,排序 arr[l..r]
public static void sort(int[] arr, int l, int r) {
if (l < r) {
// 找到中点
int m = l + (r - l) / 2;
// 排序两边
sort(arr, l, m);
sort(arr, m + 1, r);
// 合并两边
merge(arr, l, m, r);
}
}
public static void main(String[] args) {
int[] arr = {38, 27, 43, 3, 9, 82, 10};
System.out.println("Given Array");
for (int i : arr) {
System.out.print(i + " ");
}
System.out.println();
sort(arr, 0, arr.length - 1);
System.out.println("\nSorted array");
for (int i : arr) {
System.out.print(i + " ");
}
}
}
迭代版实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
public class MergeSortIterative {
// 合并两个有序子数组 arr[l..m] 和 arr[m+1..r]
public static void merge(int[] arr, int l, int m, int r) {
// 找到两个子数组的大小
int n1 = m - l + 1;
int n2 = r - m;
// 创建临时数组来存储左右子数组
int[] L = new int[n1];
int[] R = new int[n2];
// 复制数据到临时数组 L 和 R
for (int i = 0; i < n1; ++i)
L[i] = arr[l + i];
for (int j = 0; j < n2; ++j)
R[j] = arr[m + 1 + j];
// 初始索引
int i = 0, j = 0, k = l;
// 合并临时数组 L 和 R 回到 arr[l..r]
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = R[j];
j++;
}
k++;
}
// 复制 L 中剩余的元素(如果有)
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
// 复制 R 中剩余的元素(如果有)
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
// 主函数,排序 arr[0..n-1] 使用迭代的归并排序
public static void sort(int[] arr) {
int n = arr.length;
// 当前大小的子数组 curr_size,从 1 开始
for (int curr_size = 1; curr_size < n; curr_size = 2 * curr_size) {
// 选择左边子数组的起始点 left_start,逐步合并
for (int left_start = 0; left_start < n - 1; left_start += 2 * curr_size) {
// 找到中点和右边子数组的结束点
int mid = Math.min(left_start + curr_size - 1, n - 1);
int right_end = Math.min(left_start + 2 * curr_size - 1, n - 1);
// 合并子数组 arr[left_start..mid] 和 arr[mid+1..right_end]
merge(arr, left_start, mid, right_end);
}
}
}
public static void main(String[] args) {
int[] arr = {38, 27, 43, 3, 9, 82, 10};
System.out.println("Given Array");
for (int i : arr) {
System.out.print(i + " ");
}
System.out.println();
// 调用迭代版归并排序
sort(arr);
System.out.println("\nSorted array");
for (int i : arr) {
System.out.print(i + " ");
}
}
}
本文由作者按照 CC BY 4.0 进行授权