堆

堆（Heap）

堆（Heap）是一种特殊的完全二叉树，广泛应用于计算机科学中，尤其在实现优先队列和堆排序时非常有用。

定义

堆是一种特殊的完全二叉树，主要分为两种类型：

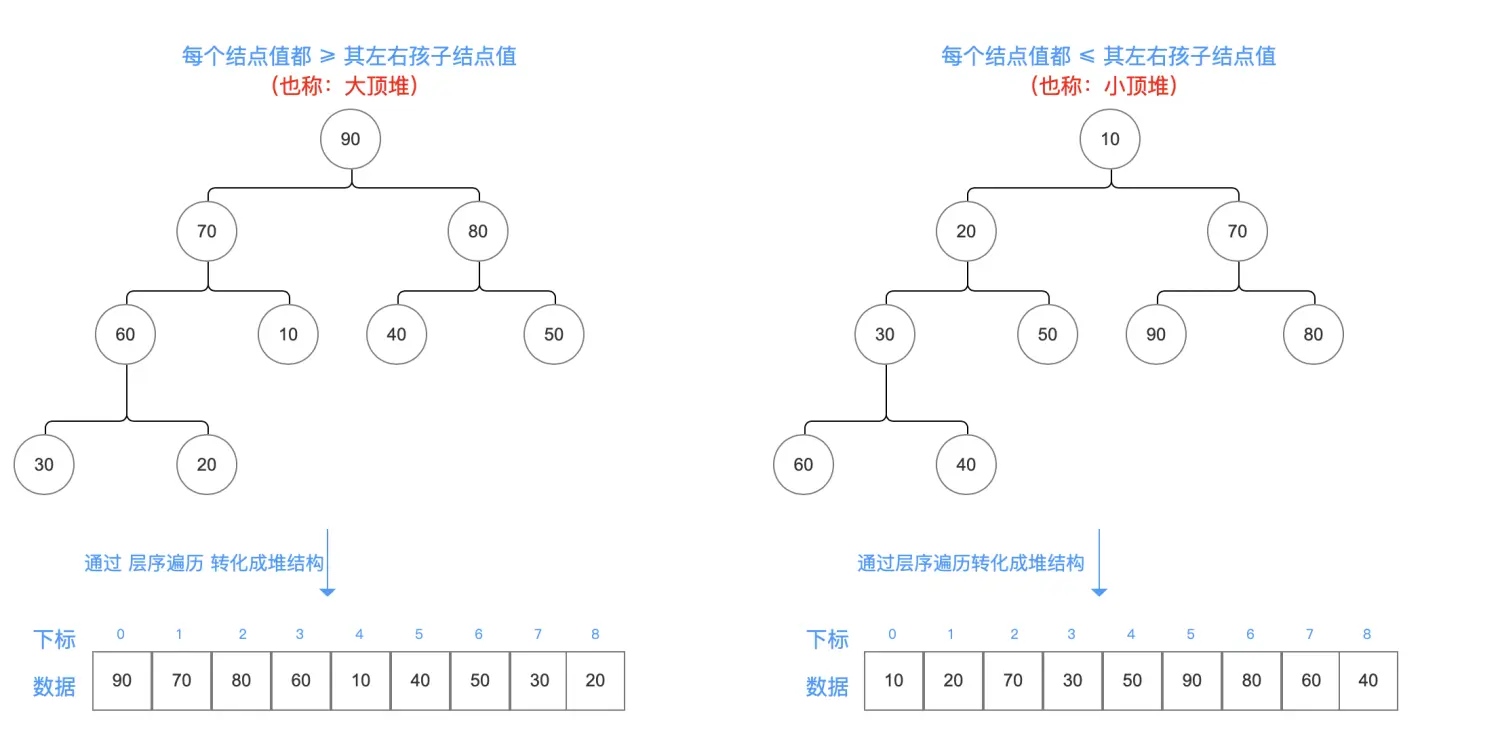
• 最大堆（Max Heap）：在最大堆中，父节点的值总是大于或等于其子节点的值。
• 最小堆（Min Heap）：在最小堆中，父节点的值总是小于或等于其子节点的值。

性质

1. 完全二叉树：堆必须是完全二叉树，这意味着树是完全填满的，只有最后一层可能不满，并且节点从左到右依次排列。
2. 堆属性：对于最大堆，任何给定节点的值总是大于或等于其子节点的值；对于最小堆，任何给定节点的值总是小于或等于其子节点的值。

实现

堆通常使用数组来实现。数组索引与堆的节点关系如下：

• 给定一个节点在数组中的索引 i：
  • 父节点的索引为 (i - 1) / 2
  • 左子节点的索引为 2 * i + 1
  • 右子节点的索引为 2 * i + 2

示例

以下是一个最大堆的示例：

在这个最大堆中，每个节点的值都大于或等于其子节点的值。

操作

插入

1. 将新元素添加到堆的末尾。
2. 调整新元素的位置以保持堆属性（向上调整，或称“上滤”）。

删除

1. 通常删除堆顶元素（最大堆的最大元素或最小堆的最小元素）。
2. 将堆的最后一个元素移到堆顶。
3. 调整堆顶元素的位置以保持堆属性（向下调整，或称“下滤”）。

堆化

将一个无序数组转化为堆。通常通过从最后一个非叶节点开始向前遍历，依次调整节点的位置来完成（构建堆的时间复杂度为 O(n)）。

应用

1. 优先队列：堆常用于实现优先队列，其中优先级最高的元素最先被处理。
2. 排序（堆排序）：利用堆的性质进行排序，时间复杂度为 O(n log n)。
3. 图算法：如 Dijkstra 算法和 Prim 算法中使用堆来找到最短路径或最小生成树。

代码示例（Java）

以下是一个最大堆的 Java 实现：

/**
 * 最大堆（MaxHeap）的实现
 */
public class MaxHeap {
    private int[] heap; // 数组实现堆
    private int size; // 堆中元素的数量

    /**
     * 初始化一个最大堆
     * @param capacity 堆的容量
     */
    public MaxHeap(int capacity) {
        heap = new int[capacity]; // 初始化数组
        size = 0; // 初始时堆中元素数量为0
    }

    /**
     * 向最大堆中插入一个元素
     * @param val 要插入的值
     */
    public void insert(int val) {
        if (size == heap.length) {
            throw new IllegalStateException("Heap is full"); // 堆已满，抛出异常
        }
        heap[size] = val; // 将新元素放在堆的末尾
        size++; // 堆大小加1
        heapifyUp(size - 1); // 调整堆以维持堆属性
    }

    /**
     * 上滤操作：调整堆以维持堆属性
     * @param index 要上滤的元素索引
     */
    private void heapifyUp(int index) {
        int parentIndex = (index - 1) / 2; // 父节点索引
        // 如果当前节点大于父节点，交换它们，继续向上直到满足堆属性
        while (index > 0 && heap[index] > heap[parentIndex]) {
            // 交换当前节点和父节点的值
            int temp = heap[index];
            heap[index] = heap[parentIndex];
            heap[parentIndex] = temp;
            // 更新当前节点索引为父节点索引，继续向上比较
            index = parentIndex;
            parentIndex = (index - 1) / 2;
        }
    }

    /**
     * 删除并返回堆顶元素（最大元素）
     * @return 堆顶的最大元素
     */
    public int extractMax() {
        if (size == 0) {
            throw new IllegalStateException("Heap is empty"); // 堆为空，抛出异常
        }
        int max = heap[0]; // 堆顶元素（最大元素）
        heap[0] = heap[size - 1]; // 将最后一个元素移到堆顶
        size--; // 堆大小减1
        heapifyDown(0); // 调整堆以维持堆属性
        return max; // 返回最大元素
    }

    /**
     * 下滤操作：调整堆以维持堆属性
     * @param index 要下滤的元素索引
     */
    private void heapifyDown(int index) {
        // 循环直到当前节点没有子节点
        while (index < size / 2) {
            int leftChild = 2 * index + 1; // 左子节点索引
            int rightChild = 2 * index + 2; // 右子节点索引
            int largest = index; // 最大值索引，默认为当前节点

            // 找出当前节点、左子节点和右子节点中的最大值索引
            if (leftChild < size && heap[leftChild] > heap[largest]) {
                largest = leftChild;
            }
            if (rightChild < size && heap[rightChild] > heap[largest]) {
                largest = rightChild;
            }

            // 如果最大值索引不是当前节点索引，则交换当前节点和最大值节点的值，并继续向下比较
            if (largest != index) {
                int temp = heap[index];
                heap[index] = heap[largest];
                heap[largest] = temp;
                index = largest;
            } else {
                break; // 已经满足堆属性，退出循环
            }
        }
    }

    // 测试示例
    public static void main(String[] args) {
        MaxHeap heap = new MaxHeap(10); // 创建一个容量为10的最大堆
        heap.insert(10); // 插入元素10
        heap.insert(20); // 插入元素20
        heap.insert(5); // 插入元素5
        System.out.println(heap.extractMax()); // 输出堆顶的最大元素（应为20）
    }
}